Более того, часто имеет смысл
Глава 1 Глава 2 Более того, часто имеет смысл из всех точек данных вычесть среднее. При этом центр распределения сместится в начало координат. В этом случае точка данных, которая смещена на одно стандартное отклонение вправо от среднего, имеет значение 1 на оси X. Если мы вычтем среднее из точек данных, а затем разделим полученные значения на стандартное отклонение точек данных, то преобразуем распределение в нормированное нормальное (standardized normal). Это нормальное распределение со средним, равным 0, и дисперсией, равной 1. Теперь N'(Z) даст нам значение на оси Y (высота кривой) для любого значения Z:
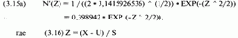U = среднее значение данных;
S = стандартное отклонение данных;
Х = наблюдаемая точка данных;
ЕХР() = экспоненциальная функция.
Уравнение (3.16) дает нам число стандартных единиц, которым соответствует точка данных; другими словами, число стандартных отклонений, на которое точка данных смещена от среднего. Когда уравнение (3.16) равно 1, оно называется стандартным нормальным отклонением (standard normal deviate) от среднего значения. Стандартное отклонение, или стандартная единица, иногда называется сигмой (sigma). Таким образом, когда говорят о событии, которое было «событием пяти сигма», то речь идет о событии, вероятность которого находится за пределами пяти стандартных отклонений.
Рисунок 3-7 показывает нормальную кривую, заданную предедущим уравнением. Отметьте, что высота стандартной нормальной кривой составляет 0,39894, поскольку из уравнения (3.15а) мы получаем:
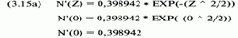Отметьте, что кривая непрерывна (в ней нет «разрывов»), когда она переходит из отрицательной области слева в положительную область справа. Отметьте также, что кривая симметрична: сторона справа от пика является зеркальным отражением стороны слева. Предположим, у нас есть группа данных, где среднее равно 11, а стандартное отклонение равно 20. Чтобы увидеть, где точка данных будет отображена на кривой, рассчитаем ее в стандартных единицах. Предположим, что рассматриваемая точка данных имеет значение -9. Чтобы рассчитать число стандартных единиц, мы сначала должны вычесть среднее из этой точки данных: - 9- 11 =-20
Затем надо разделить полученный результат на стандартное отклонение:
-20/20=-1
